資料結構-複雜度計算

發表於 2025-06-23 更新於 2025-06-28

前情提要

在準備研究所面試與專題報告時，演算法分析 往往是必考重點。本文彙整了從最基礎的漸進符號定義（O, Ω, Θ, o, ω）到空間複雜度、遞迴關係、以及Master 定理與其擴展版本的精華內容，並搭配典型範例與 C/C++ 實作要點，助你快速掌握：

各種 Asymptotic Notation 的嚴謹定義與相互關係
空間複雜度 分析要點與 C/C++ 參數傳遞差異
遞迴函式 的展開帶入法與 Master 定理（原始／擴展）
限定與推導法（Limit Method）、等價證明、Log Method 常見技巧
典型範例：Selection Sort、階乘、遞迴和遞迴樹、Stirling 公式等

無論你是研究所考生、面試準備者，或想系統複習演算法理論的工程師，這篇筆記都能提供一個清晰、一站式的參考架構。讓我們從基本概念出發，一步步深入最核心、最實用的分析技巧！

Introduction

Definition by Algorithm: An algorithm is a finite set of instructions that if followed, accomplishes a particular task . In addition, all algorithms must satisfy the following criteria.
演算法是一組有限的指令集合，若依序執行，便能完成某項特定任務。此外，所有演算法必須符合以下幾項條件。

Input. Zero or more quantities are externally supplied. 輸入零個或是多個數值
output. 演算法必須產生至少一個結果。
definiteness(確定性). Each instruction must be clear and unambiguous.每一條指令都必須是明確且無歧義的，不能讓執行者產生混淆。
finiteness(有限性). 演算法必須在有限步驟內結束，不能無限執行。
effectiveness(有效性) .每一條指令都必須是非常基本的，以至於理論上人類只用紙筆就能執行它。僅僅像第三項（criterion 標準確定性）那樣定義清楚還不夠；它還必須是可行的（實際能做到的）。

Selection sort algorithm
- 找到最小的元素(a[j])，交換當前的元素(a[i]) tmp := a[i]; a[i] := a[j]; a[j] := tmp;

Algorithm SelectionSort(a,n)
{
 for i := 1 to n do
 {
  j:=i;
  for k=i+1 to n do
   if (a[k] < a[j]) then j:=k;
  tmp:=a[i]; a[i]:=a[j]; a[j]:=tmp;
 }
}

C 與 C++ 的參數傳遞

在 C/C++ 中，參數傳遞方式會影響變動空間需求：

C style 陣列
- 函式參數 int A[] 或 int A[100] 都退化為 int* A（指標），表示傳址（call-by-address），不會複製陣列。
- 若要模擬 call-by-value（複製整個陣列），必須手動分配並 memcpy：
  1
  2
  3
  4
  5
  6
  void bar_by_value(int A[], int n) {
  int* copy = (int*)malloc(n * sizeof(int));
  memcpy(copy, A, n * sizeof(int));
  // SP(I) = Θ(n)
  free(copy);
  }
- 直接傳指標時：
  1
  2
  3
  void bar_by_address(int A[], int n) {
  // SP(I) = Θ(1)
  }
C++ 容器（std::vector / std::array）
- 值傳遞 std::vector<int> v：會複製底層陣列 → SP(I) = Θ(n)
- 參考傳遞 const std::vector<int>& v：不複製 → SP(I) = Θ(1)
- 同理，std::array<int,N> 若以值傳遞亦會複製整個陣列物件。
C++ 真參考（reference）
- 使用 int& x：純參考傳遞，可直接修改呼叫端變數 → SP(I) = Θ(1)
- 與指標類似，但語法更直觀。

void incrementRef(int& x) {
  x++;
}

int main() {
  int a = 5;
  incrementRef(a);
}

C++ 指標傳遞（Call-by-Address）
- 使用指標參數，直接傳入變數位址 → 不複製資料

void increment(int* x) {
  (*x)++;
}

int main() {
  int a = 5;
  increment(&a);
}

Asymptotic notation

Definition

g(n) 是指一個基準還數有可能是nlog(n) 或是 log(n)的基準
O(g(n)) = {f(n) ∣ ∃ c > 0, ∃ n₀ > 0, ∀n ≥ n₀, 0 ≤ f(n) ≤ c ⋅ g(n)}
1. 表示某個函數 f(n) 增長速度「最多不會超過」**某個基準函數 g(n) 的常數倍，當 n ≥ n₀ 時就一直成立。
2. 可使為上界。
o(g(n)) = {f(n) ∣ ∃ c > 0, ∃ n₀ > 0, ∀n ≥ n₀, 0 ≤ f(n) < c ⋅ g(n)}

嚴格上屆

Ω(g(n)) = {f(n) ∣ ∃ c > 0, ∃ n₀ > 0, ∀n ≥ n₀, f(n) ≥ c ⋅ g(n)}

表示某個函數 f(n) 增長速度「會超過」某個基準函數 g(n)的長數倍數，當 n ≥ n₀ 時就一直成立。
可視為下界。

ω(g(n)) = {f(n) ∣ ∃ c > 0, ∃ n₀ > 0, ∀n ≥ n₀, f(n) > c ⋅ g(n)}

嚴格下界

Θ(g(n)) = {f(n) ∣ ∃ c₁ > 0, ∃ c₂ > 0, ∃ n₀ > 0, ∀n ≥ n₀, c₁ ⋅ g(n) ≤ f(n) ≤ c₂ ⋅ g(n)}

表示 f(n) 的增長速度恰好等同於 g(n)，也就是它上下都被 g(n) 的常數倍包住。
可是為中間上下界都有。

❗️如果 f(n) < g(n)，不代表 f(n) 的 growth order 比 g(n) 的 growth order 小是不正確的
❗️如果兩個 asymptotic natations 相加取大的那個

Attribute

Asymptotic notation	屬性	說明
Θ, Ω, O, o, ω	遞移性(Transitivity)	若 f 與 g 風格相同，且 g 與 h 也相同，那麼 f 與 h 也相同。 Θ, Ω, O, o, ω 都有這個性質。
Θ, Ω, O	返身性(Reflexivity)	函數必然和自己相同階。 Θ, Ω, O 滿足f = Θf、f = Ωf、f = Of。但 o、ω 因為是「嚴格」關係（f = og 不允許 f = ωg），不具返身性。
Θ	對稱性(Symmetry)	若 f 同階於 g，則 g 也同階於 f。只有 Θ 有「完全對稱性」。
Ω, O, o, ω	變換對稱性(Transpose Symmetry)	這是一種「換位也成立」的弱對稱──例如 f = O(g) 等價於 g = Ω(f) f = o(g) 等價於 g = ω(f) 這四種符號都具備這個互換關係。

Trichotomy

漸進符號關係不滿足三分律：對任意兩個函數 (f, g)，不一定 存在且僅存在下列三種之一： f = O(g) ∨ f = Θ(g) ∨ f = Ω(g).

不可比（Incomparable）：有時既不是 (f=O(g))，也不是 (g=O(f))。
範例：令l f(n) = n, g(n) = n^{1 + sin (n)}, 由於 1 + sin n 在 [0,2] 間震盪，無法統一找到常數 c, n₀ 使其中一邊恆成立，故這對函數不可比。

Limit Asymptotic Theorem

$$ \lim_{n \to \infty} \frac{f(n)}{g(n)} = L \quad\Longrightarrow\quad \begin{cases} L = 0: & f(n) = o(g(n)) \\ L = C \in (0, \infty): & f(n) = \Theta(g(n)) \\ L = \infty: & f(n) = \omega(g(n)) \end{cases} $$

值 (L)	關係	結論
0	嚴格上界，f 成長遠慢於 g	f(n) = o(g(n))
C ∈ (0,∞)	精確階，f 成長剛好等同 g	f(n) = Θ(g(n))
∞	嚴格下界，f 成長遠快於 g	f(n) = ω(g(n))

範例

$$ \lim_{n \to \infty} \frac{f(n)}{g(n)} = \lim_{n \to \infty} \frac{n^2 + n + 1}{n^3} = \lim_{n \to \infty} \Bigl(\frac1n + \frac1{n^2} + \frac1{n^3}\Bigr) = 0 $$

根據極限定理，得到 f(n) = o(g(n))

範例：f(n) = 3n² − 100n + 6 屬於 ω(n) {106 中原資工}

$$ \lim_{n\to\infty}\frac{f(n)}{n} = \lim_{n\to\infty}(3n - 100 + \tfrac{6}{n}) = \infty \quad\Longrightarrow\quad f(n) = \omega(n) $$

範例：(n+a)^b 是否屬於 Θ(n^b)，且 b 是一個 real constants {106 中原資工}

$$ \lim_{n \to \infty} \frac{(n + a)^b}{n^b} = \lim_{n \to \infty} \frac{n^b\,(1 + \tfrac{a}{n})^b}{n^b} = \lim_{n \to \infty}\bigl(1 + \tfrac{a}{n}\bigr)^b = 1 $$

實際上 (n+a)^b = Θ(n^b) ⇒ True。

Log Method

log(f(n)) = o(log(g(n))可保證f(n) = o(g(n))
log(f(n)) = ω(log(g(n))可保證f(n) = ω(g(n))
但不保證 log f(n) = Θ(log g(n))

$$ \begin{aligned} &\text{Let}\; f(n)=2^{\lg n},\quad g(n)=n^3,\\ &\lg f(n) =\lg\bigl(2^{\lg n}\bigr) =(\lg n)\,(\lg 2) =\lg n,\\ &\lg g(n) =\lg(n^3) =3\,\lg n,\\ &\therefore\quad \lg f(n)=\Theta\bigl(\lg g(n)\bigr), \quad\text{but}\quad f(n)=o\bigl(g(n)\bigr)\,. \end{aligned} $$

各種等價證明

等價 of O, Ω and Θ

(f(n) = O(g(n)) ∧ f(n) = Ω(g(n))) ⇔ f(n) = Θ(g(n)) $$ \begin{aligned} \text{Proof:}\\ (\Rightarrow)\quad &\exists\,C_2,n_2:\;\forall n\ge n_2,\;f(n)\le C_2\,g(n),\\ &\exists\,C_1,n_1:\;\forall n\ge n_1,\;f(n)\ge C_1\,g(n),\\ &n_0=\max(n_1,n_2),\quad c_1=C_1,\;c_2=C_2,\\ &\forall n\ge n_0:\;c_1\,g(n)\le f(n)\le c_2\,g(n) \;\Longrightarrow\;f(n)=\Theta(g(n)).\\ (\Leftarrow)\quad &\text{From }\Theta\text{ definition: }c_1g(n)\le f(n)\le c_2g(n)\ (\forall n\ge n_0),\\ &\text{drop lower bound }\Rightarrow f(n)=O(g(n)),\quad \text{drop upper bound }\Rightarrow f(n)=\Omega(g(n)). \end{aligned} $$

複雜度小不代表每一個 n 的時候就會比較少的執行時間
也不能給 n 一個數值，說某個演算法比另一個快，因為有可能 n 不夠大

Big-O 運算的封閉性（加法 & 乘法）

f(n) = O(s(n)) ∧ g(n) = O(r(n)) ⇒ f(n) + g(n) = O(s(n)+r(n)) 『特性 1.2』

$$ \begin{aligned} &f(n)=O(s(n))\wedge g(n)=O(r(n))\\ &\Longrightarrow \exists\,C_1,n_1:\;\forall n\ge n_1,\;0\le f(n)\le C_1\,s(n),\\ &\quad\quad\; \exists\,C_2,n_2:\;\forall n\ge n_2,\;0\le g(n)\le C_2\,r(n).\\ &\text{Let }n_0=\max(n_1,n_2),\;C=C_1+C_2.\\ &\forall n\ge n_0:\quad f(n)+g(n)\le C_1\,s(n)+C_2\,r(n)\le C\bigl(s(n)+r(n)\bigr).\\ &\Longrightarrow\;f(n)+g(n)=O\bigl(s(n)+r(n)\bigr). \end{aligned} $$

f(n) = O(s(n)) ∧ g(n) = O(r(n)) ⇒ f(n) ⋅ g(n) = O(s(n)⋅r(n)) 『特性 1.2』

$$ \begin{aligned} &f(n)=O(s(n)) \wedge g(n)=O(r(n))\\ &\Longrightarrow \exists\,C_1,n_1:\;\forall n\ge n_1,\;0\le f(n)\le C_1\,s(n),\\ &\quad\quad \exists\,C_2,n_2:\;\forall n\ge n_2,\;0\le g(n)\le C_2\,r(n).\\ &\text{Let }n_0=\max(n_1,n_2),\quad C=C_1\cdot C_2.\\ &\forall n\ge n_0:\quad f(n)\cdot g(n)\le (C_1\,s(n))\,(C_2\,r(n))=C\bigl(s(n)\,r(n)\bigr).\\ &\Longrightarrow\;f(n)\cdot g(n)=O\bigl(s(n)\,r(n)\bigr). \end{aligned} $$

f(n) = O(g(n)) ⇒ f(n) + g(n) = O(g(n)) 『特性 1.3』

$$ \begin{aligned} &f(n)=O(g(n)) \;\Longrightarrow\; \exists\,C>0,\;n_0:\;\forall n\ge n_0,\;f(n)\le C\,g(n),\\ &\therefore\; f(n)+g(n)\le Cg(n)+g(n)=(C+1)\,g(n),\\ &\Longrightarrow\; f(n)+g(n)=O(g(n)). \end{aligned} $$

Space Complexity

總空間需求
SP(P) = c + SP(I)
- c：程式本身或固定配置所需的常數空間
- SP(I)：變動空間需求（分析時重點）
變動空間 SP(I) 包含
1. 資料結構本身：動態配置的陣列、物件、鏈結串列、樹⋯⋯
2. 參數傳遞
  - Call-by-value：值會複製 → 可能需要 O(n) 空間
  - Call-by-address/reference：只傳位址 → O(1) 空間
3. 遞迴呼叫棧：每層呼叫的參數與局部變數都要壓到呼叫棧上
分析重點
- 忽略常數 c，只看 SP(I) 隨 n 增長的量級
- 若無動態結構也不遞迴 → SP(I) = O(1)
- 若遞迴深度為 d，每層 O(1) → SP(I) = O(d)
- 若動態配置長度為 n 的陣列 → SP(I) = O(n)

範例

純迴圈、無動態配置 SP(I) = O(1)

void foo(int n) {
    int x = 0;
    for (int i = 0; i < n; i++) {
        x += i;
    }
}

遞迴計算階乘 n ⇒ SP(I) = O(n)

int fact(int n) {
    if (n <= 1) return 1;
    return n * fact(n - 1);
}

call-by-address(reference) SP(I) = O(1) vs. call-by-value SP(I) = O(n)

void bar(int A[], int n);         

void bar(int B[], int n) {        
    int* copy = new int[n];
    // ...
}

Time complexity

Stirling’s Formula

$$ n! \;\sim\; \sqrt{2\pi n}\,\left(\frac{n}{e}\right)^{n} $$

或更精確帶誤差項： $$ n! \;=\; \sqrt{2\pi n}\,\left(\frac{n}{e}\right)^{n} \;\Bigl(1 + O\bigl(\tfrac1n\bigr)\Bigr) $$

Growth rate (fast to slow)

函數 (Function)	級距 (Category)	證明？
2^2ⁿ, 2^{2^n + 1}	指數 × 指數 (Double Exponential)	✅
n!, (n+1)!	階乘 (Factorial)	✅
eⁿ, n 2ⁿ, 2ⁿ, (3/2)ⁿ	指數 (Exponential)	✅
(lgn)^lg n = n^lg lg n, (lgn)!	超多項式 (Super polynomial)	✅
$n^3,n^2=4^{\lg n},\;n\lg n,\;\lg(n!),\;n=2^{\lg n},\;\sqrt{n}=(\sqrt2)^{\lg n}$	多項式 (Polynomial)	❌
$\displaystyle\frac{2^{\sqrt{2\,\lg n}}}{\lg^2 n}$	次多項式 (Sub polynomial)	✅
(lgn)^k, (lnn)^k	多對數 (Poly-log)	❌
$\lg n,\;\ln n,\;\sqrt{\lg n},\;\ln\ln n$	對數 (Logarithmic)	❌
lg^n, lg^(lgn) + 1, lg (lg^*n)	迭代對數 (Iterated Logarithm)	✅
n^1/lg n = 2, 1	常數 (Constant)	❌

Prove (lgn)!

$$ \begin{aligned} (\lg n)! &\approx \sqrt{2\pi\,\lg n}\Bigl(\tfrac{\lg n}{e}\Bigr)^{\lg n} \quad(\text{套用 Stirling 公式})\\ &= \sqrt{2\pi}\,(\lg n)^{\lg n+\tfrac12}e^{-\lg n} \quad(\text{整理根號與指數項})\\ &\sim (\lg n)^{\lg n+\tfrac12}e^{-\lg n} \quad(\text{忽略與 $n$ 無關之常數 $\sqrt{2\pi}$})\\ &= (\lg n)^{\lg n}\sqrt{\lg n}\;e^{-\lg n} \quad(\text{拆分指數與根號})\\ &= (\lg n)^{\lg n}\sqrt{\lg n}\;\frac1n \quad(\substack{\text{因為 }e^{-\lg n}=1/n\,,\\\text{若$\lg=\ln$則顯然，或換底後亦可得此式}})\\ &= \frac{(\lg n)^{\lg n+\tfrac12}}{n} \quad(\text{得到最終漸近形式}) \end{aligned} $$ 證明意義：由
$$ (\lg n)! \sim \frac{(\lg n)^{\lg n+\tfrac12}}{n} $$
可得
$$ \begin{aligned} (\lg n)^{\lg n}\times\frac1n\times\sqrt{\lg n} &\;\downarrow\;(\text{捨棄 }\sqrt{\lg n})\\ (\lg n)^{\lg n}/n &\;\downarrow\;(\text{換底＋指數恆等式})\\ n^{\log\log n}/n &\;\downarrow\;(\text{捨棄 }1/n\text{ 次要因子})\\ n^{\log\log n} \end{aligned} $$

**Prove n^1/lg n = 2

$$ \begin{aligned} n &= 2^{\lg n},\\ \therefore\quad n^{\frac1{\lg n}} &= \bigl(2^{\lg n}\bigr)^{\frac1{\lg n}} = 2^{(\lg n)\cdot\frac1{\lg n}} = 2. \end{aligned} $$

Prove log (n!) = Θ(nlogn)

簡單來說就是 O 是利用每一項都最小於 Ω 利用數列的後半段當作原本函數的下界，再利用每一項都大於最小項求得。 $$ \begin{aligned} \log(n!) &= \log n + \log(n-1) + \cdots + \log1 \;\underset{\forall\,k:\,\log k\le\log n}{\le}\;n\log n \;\;\Rightarrow\;\; \log(n!)=O(n\log n), \\[6pt] \log(n!) &= \log n + \log(n-1) + \cdots + \log1 \;\ge\;\underbrace{\log n + \log(n-1) + \cdots + \log\bigl(\tfrac n2\bigr)}_{\,\text{取後半 }n/2\text{ 項，並且最後選擇 n/2 項}}\\ &\;\underset{\forall\,k>\tfrac n2:\,\log k\ge\log(n/2)}{\ge}\;\frac n2\,\log\!\Bigl(\tfrac n2\Bigr) \;\;\Rightarrow\;\; \log(n!)=\Omega(n\log n), \\[6pt] &\qquad\Longrightarrow\quad \log(n!)=\Theta(n\log n). \end{aligned} $$

範例：Let $T(n) = 1 + \frac12 + \frac13 + \cdots + \frac1n$ and assume T(n) = Θ(f(n)). Derive the simplest formula for f(n).

$$ \begin{aligned} T(n)&=\sum_{k=1}^n\frac1k \;\le\;\int_1^n\frac{1}{x}\,dx+1 \;=\;\ln n+1 \;=\;O(\ln n),\\ T(n)&=\sum_{k=1}^n\frac1k \;\ge\;\int_1^{n+1}\frac{1}{x}\,dx \;=\;\ln(n+1) \;=\;\Omega(\ln n),\\ \therefore\;T(n)&=\Theta(\ln n) \;\Longrightarrow\; f(n)=\ln n. \end{aligned} $$

Recursive Time function

展開帶入法

考慮遞迴
T(n) = 2 T(n−1) + 1, T(1) = 1.

對 T(n) 連續展開 k 次：
$$ \begin{aligned} T(n) &=2\,T(n-1)+1\\ &=2\bigl(2\,T(n-2)+1\bigr)+1 =2^2\,T(n-2)+(2^1+2^0)\\ &=2^2\bigl(2\,T(n-3)+1\bigr)+(2^1+2^0) =2^3\,T(n-3)+(2^2+2^1+2^0)\\ &\;\;\vdots\\ &=2^k\,T(n-k)+\sum_{i=0}^{k-1}2^i =2^k\,T(n-k)+(2^k-1). \end{aligned} $$

令 k = n − 1，則 T(n−k) = T(1) = 1，得到
T(n) = 2^n − 1 ⋅ 1 + (2^n − 1 − 1) = 2 ⋅ 2^n − 1 − 1 = 2ⁿ − 1.

Master Theorem

Master Theorem 就是一種 直接求解 以下形式遞迴關係的工具： T(n) = aT(n/b) + f(n), a ≥ 1, b > 1 它特別 適用於 分治（Divide & Conquer）演算法，因為這類演算法通常會把一個大小為 n 的問題，切成 a 個大小約為 n/b 的子問題，然後再做額外的合併工作 f(n)，這邊的 b 只有 > 的原因是因為他是切割幾個子問題那麼就需要只寫 >，不然就沒有切割問題了，主要比較的是 n^log_ba 和 f(n) 在比較。

下圖為解釋 nlog_ba 由來

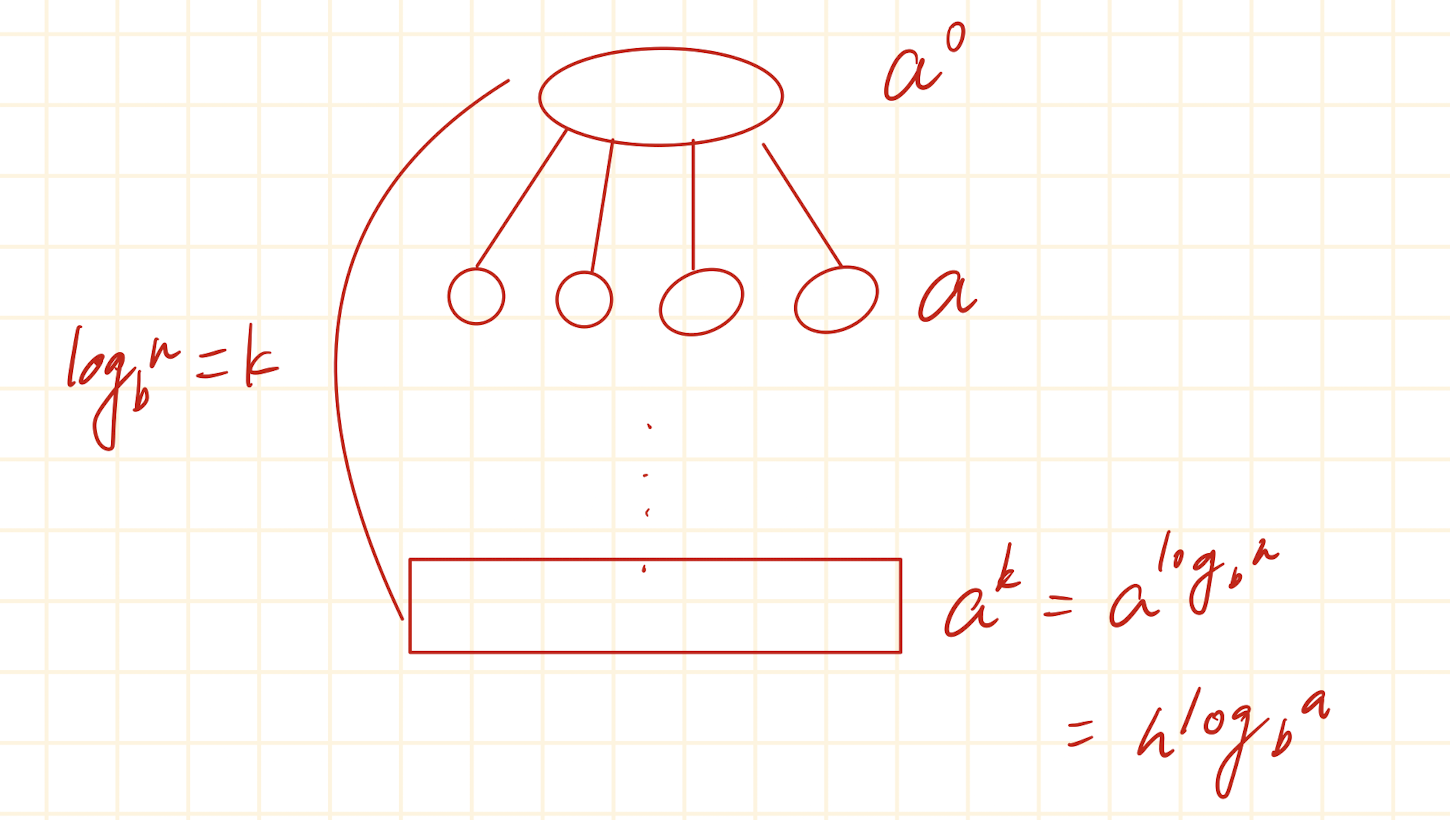
case 1 : if f(n) = O(n^{log_ba − ε}), ε > 0 ⇒ θ(n^log_ba)
case 2 : if f(n) = O(n^log_ba) ⇒ θ(n^log_balgn)
case 3 : if f(n) = Ω(n^{log_ba + ε}), ε > 0 and af(n/b) ≤ cf(n), 0 > c > 1, ∀n ⇒ T(n) = Θ(f(n))

Extended Master Theorem

為何要使用：原始 Master 定理的 Case 2 只處理
f(n) = Θ(n^log_ba)
這種「純多項式」情況，無法涵蓋像 nlog n 這種 在臨界階 n^log_ba 上額外乘 log n 的形式。

若
f(n) = Θ(n^log_ba log^kn), k ≥ 0,
則
T(n) = a T(n/b) + f(n) = Θ(n^log_ba log^k + 1n).

範例：
$$ T(n)=2\,T\bigl(\tfrac n2\bigr)+n\log n. $$
此時 a = 2、b = 2，臨界階 n^log₂2 = n，而
f(n) = nlog n = Θ(n¹log¹n)
對應 k = 1。
原始 Master 定理 嘗試比較的是 n¹ 與 nlog n，可發現 Case 1/2/3 均不符合：

Case 1 要求 nlog n = O(n^1 − ε) → 不成立
Case 2 要求 nlog n = Θ(n) → 不成立
Case 3 要求 nlog n = Ω(n^1 + ε) → 不成立

故必須使用 Extended Master，代入 k = 1 得
T(n) = Θ(n¹ log²n) = Θ(nlog²n).